Optimization
Stanford CVX
BA
Optimization Methods for Business Analytics
15-053-optimization-methods-in-management-science Learn how to use optimization methodologies and modeling approaches to effectively analyze data.
Open Solver
Can install by the same way we add solver in Excel.
The Simplex Method for a maximization problem moves from extreme point to extreme point while increasing the objective value.
The simplex algorithm terminates if this occurs and simplex is guaranteed to terminate at an optimum solution if the problem is feasible.
There are two extreme points: (0, 0) and (0, 1).
There are two extreme rays. The first is the set of points {(λ,0):λ≥0}. The second is the set of points {(λ,1+λ):λ≥0}.
Because each term of the objective function is guaranteed to be nonnegative, there can be no better solution. Note that (1,2) is not an extreme point of the feasible region. When optimizing a nonlinear function, the optimum is not guaranteed to occur at an extreme point.
A good way to determine which one to store is to solve the problem five additional times. The first problem includes one extra storage unit for chicken. The second problem includes one extra storage unit for beef. And so on. If you do this, you will find that storing 1 extra kg of tofu increases the profit the most. There are other approaches for solving this problem. Next week, we will learn integer programming models. It is possible to write a single model for finding the solution. In the fifth week of this course, you will learn about sensitivity analysis. You can determine the answer from the sensitivity report.
The point of Problem 1 is that there are multiple ways of representing integer programs. Some are better in practice because they help the algorithm to find the optimum faster.
Select the correct way of modeling this “OR” constraint using linear and integer constraints.
Consider two non-negative integral variables x1 and x2. Suppose that x1≤60 and x2≤50. Model the following constraint using an additional binary variable w:
x1<30 or x2≥20.
It is often difficult to work with strict inequalities when modeling MIPs (Mixed Integer/Linear Programs). In this case, x1 is known to be integer valued. We transformed “x1<30” into “x1≤29.”
In order to make the constraint x1≤29+M(1−w) redundant when w=0, one needs M to be at least 31. In order to make the constraint x2≥20–Mw be redundant when w=1, we need M to be at least 20.
A basketball coach is trying to come up with a team for the following match. He has a total of 9 players from which he must select 5 . Assume these 5 players will play the whole game. Consider there are three positions players can play: guard, forward, and center. So the team of 5 players will consist of 2 guards, 2 forwards, and 1 center. Players 1,2,3,4,8,9 can play guard, 3,4,5,6,7,8,9 can play forward, and 8,9 can play center.
Consider the decision variables as xi for i∈{1,…,9} so that xi=1 if the coach selects player i , and xi=0 otherwise and examine the IP below. Note that since there is no objective, we state the linear objective as 0.
The IP formulated below requires that we select five players, and that at least two of these five can play guard; at least two can play forward; at least one can play center. If we solve this integer program, and obtain a feasible integer solution, is the solution guaranteed to produce a feasible five person team?
False
The above IP isn’t a correct formulation for our problem. The constraints do ensure that we have 5 players, 2 of which can play guard, 2 forward and 1 center. However, it doesn’t guarantee that we can take these five players (from the optimal solution) and assign two of them as forwards, two of them as guards and the remaining player as center.
For instance, consider the solution that picks players 5,6,7,8,9. Players 5, 6 and 7 can only play forward. That means that the two guards and the center must be chosen from the remaining two players, which is impossible.
Historical note: The above false formulation for the basketball problem was (incorrectly) given as the answer by the staff of 15.053 for a quiz in 15.053. If you didn’t see why this model was incorrect, you are definitely not alone.
Which of the statements or constraints below is (by itself) equivalent to the statement “If x1=1, then x2=0”?
Integer Programming Formulation, eHarmony
eHarmony is an online dating site focused on long term relationships. It takes a scientific approach to love and marriage. About nearly 4% of US marriages in 2012 are a result of eHarmony. The company has generated over $1 billion in cumulative revenue from 2000, the year it was founded. Unlike other online dating websites, eHarmony does not have users browse others’ profiles. Instead, eHarmony computes a compatibility score between two people and uses optimization algorithms to determine their users’ best matches. In this problem, we are going to see how eHamony uses integer programming to find good matches. The compatibility scores in the table below indicates how compatible a match is. A higher number indicates that the compatibility is greater.
A combinatorial auction is an auction in which participants can place bids on sets of items, instead of placing bids on individual items. A combinatorial auction is useful in many situations. For example, consider the problem of an airline company buying takeoff and landing slots at an airport: clearly, the value of a single slot may be small if the slot is taken by itself, but the value may be much larger if several slots can be bought at the same time, allowing the company to setup flight routes according to the desired timetable. Thus, the airport wants to sell its available slots to airline companies maximizing its own profit (i.e. the total value at which the slots are sold), allowing airlines to bid on sets of items and choosing the most profitable combination of bids among the received ones. Many other examples exist. In this problem, we study a simple formulation for a combinatorial auction.
The local post office requires full-time employees to meet demands that vary from day to day. The number of full-time employees required on each day is given in Table 1. Each full-time employee must work five consecutive days and then receive two days off. For example, an employee who works Monday to Friday must be off on Saturday and Sunday. This schedule for employees repeats every week. We want to formulate an integer program that the post office can use to minimize the number of full-time employees who must be hired.
the game of Fiver
This problem will be based on the game of Fiver. It is also sometimes called called Lights Out and you can try your hand at the game here and for more details check out the Wikipedia page here.
Assume we have a 5x5 grid that initially consists of all white blocks. When we click on a block, it flips its color (from white to black or from black to white) and that of adjacent (vertical and horizontal) blocks. Can you make all of the blocks black? The game is illustrated in this figure. For a documented illustration, click here.
We wish to write an optimization problem whose solution solves the problem in the fewest moves.
We will model it is an integer program. Let x(i,j)≥0 denote the number of times we click on the block in row i and column j.
Consider the element in row 3, column 2 again. Using the results from PARTS A, B, and C, write a constraint that guarantees it turns black. For the answers, assume that there is a constraint x(i,j)+x(i,j−1)+x(i,j+1)+x(i−1,j)+x(i+1,j)=w(i,j) Assume also that x(i′,j′) is binary for all i′,j′ and y(i,j)∈{0,1,2} .
Perhaps one could express it more succinctly in a manner similar to the way that the constraint in PART D is given. Ideally, one would only need to write a constraint for Block(i,j) and let i vary from 1 to 5 and let j vary from 1 to 5. One runs into a difficulty though. The constraint for Blocks (1, 1) includes just three of the x decision variables. It would be
where all four of these variables are binary. (Do you see why y(1,1) can be restricted to be binary?) Similarly for Blocks (1, 5), (5, 1) and (5, 5). Other Blocks in which i or j = 1 or 5 include 4 decision variables. It would seem difficult to be able to express all 25 constraints very succinctly.
However, there is a way to do so. It involves creating “dummy decision variables.” How many additional dummy variables do you think are needed? HINT: it is more than 23 and less than 25. (Yes, the previous question was intended as a joke. But now that you know the answer, see if you can figure out a clever way of writing the constraints succinctly if you are allowed the 24 extra dummy variables. This number arises because 72−52=24. The explanation for this exercise will be given when the solutions for the problem set are released.)
More on OR Exercise
Consider three binary variables , on decision variable . Select three constraints that ensures that
SOLUTION
x1=13w1+39w2+88w3
w1+w2+w3=1
w1,w2,w3∈{0,1}
Suppose that we want at least two of the following set of constraints to hold: x1≥20,x2≤6,x3≥16,x4≤18. Write the model as an integer program. Select all of the contraints below that are constraints of your linear program.
Solution
The correct answer is:
x1≥20−M(1−w1)
x2≤6+M(1−w2)
x3≥16−M(1−w3)
x4≤18+M(1−w4)
w1+w2+w3+w4≥2
w1,w2,w3,w4∈{0,1}
Divisibility Constraints
Divisibility Constraints Exercise
Consider the statement x1 is NOT divisible by 8. We model the statement starting with the constraint: x1=8y1+y2 for x1,y1,y2∈Z≥0. Which two additional constraints are needed?
SOLUTION
y2≥1.
y2≤7.
Union of Polyhedra
Fixed Charge Problems
Fixed Charge Problems Exercise
Consider the DTC problem in which S shields and K slingshot kits are produced, and suppose the fixed costs for making these are 10 and 5, respectively. Recall that the original objective was 3S+5K, with demands of 30 and 40 for shields and slingshot kits, respectively. Let w1,w2 be binary variables equal such that
w1=1 if there is a setup for shields
w1=0 otherwise no setup for shields
w2=1 if there is a setup for slingshot kits
w2=0 otherwise no setup for slingshot kits
Determine the new objective and constraints necessary for modeling the fixed charge
SOLUTION
MAX y1+y2
y1=−10w1+3S
0≤S≤30w1
y2=−5w2+5K
0≤K≤40w2
Piecewise Linear Costs Exercise
Suppose we have the following piecewise linear function of x
y=2x3 if 0≤x≤3
y=2 if 3≤x≤7
Select the necessary constraints for the formulation
SOLUTION
w1+w2=1. For the two cases
0≤x1≤3w1. Here x1 can be non-zero only if w1 is non-zero y1=2x13. The first function
y2=2w2. The second function is non-zero only if w2 is non-zero
y=y1+y2. Exactly one of the two functions must be non-zero
3w2≤x2≤7w2. Here x2 can be non-zero only if w2 is non-zero
x=x1+x2. One of the two endpoints for the domain must hold.
w1,w2∈{0,1}. Binary variables
Overview of Combinatorial Problems
Set Covering 1
There are two different solutions to the 053 Chocolate problem with three stores. Find one of these solutions.
What is the sum of the district numbers of the three stores?” (Your answer will be correct regardless of which of the two solutions you found.)
Solution
The correct answer is either 25 or 26
26, from 2, 11, and 13 25, from 4, 6, and 15
Set Covering 2
Solution
The correct answer is either 25 or 26
26, from 2, 11, and 13 25, from 4, 6, and 15
Set Packing
Set Packing Exercise
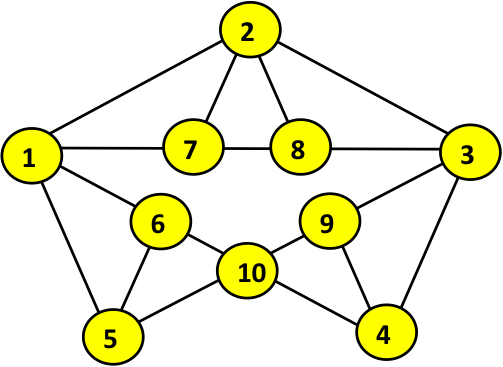
Consider the graph in the diagram below. What is the maximum size of an independent set (packing)?
Solution
The correct answer is: 3. There are various examples of packings of size 3, including (1, 3, 10), (2, 4, 5), and (2, 4, 6).
Facility Location
Facility Location 1 Exercise
Suppose that students are not required to dine, and let vs be the number of such students. If a student at location s chooses not to dine, then the disutility for that student is gs. How would the model change if this possibility were permitted? Select one objective and two constraints.
Solution
The correct answer is:
New objective: ∑d inDfdyd+∑s∈S∑d∈Dcsdxsd+∑s∈Sgsvs. We are minimizing, and so we should add the disutility.
New constraint: ∑d∈Dxsd+vs=ns for s∈S. For each location s∈S, vs is equal to the number of students at location s who do not dine at one of the facilities.
New constraint: vs≥0 for s∈S.
Graph Coloring
#Define model
m = Model()
# Assign binary values to items
#I got the right answer by stating the constraint in the variable definition. I also used @variables and @constraints to avoid repetitive code.
#, Int
@variables(m, begin
x[1:5] >= 0
y[1:5], Bin
end)
require = [ 250 300 150 200 350 180]
# Constraint on total weight
@constraint(m, x[1]+ x[2] >= require[1])
@constraint(m, x[1]+ x[3] >= require[2])
@constraint(m, x[3]+ x[2] >= require[3])
@constraint(m, x[4]+ x[2] >= require[4])
@constraint(m, x[3]+ x[5] >= require[5])
@constraint(m, x[4]+ x[5] >= require[6])
@constraint(m, x[4]+ x[5] >= require[6])
#It seems that this construct also works:
@constraint(m, x .<= 300*y)
#@constraint(m, x[1:5] .<= 300*y[1:5])
#Note the decimal point preceding the < symbol
@objective(m, Min, 450*sum{y[i], i=1:5}+2*sum{x[i], i=1:5});
# Solve model
solve(m)
# Determine which items to carry
println("Variable x Values: ", getvalue(x))
println("Variable y Values: ", getvalue(y))
# Determine value from items carried
println("Objetive value: ", getobjectivevalue(m))
he correct answer is:
x1≥300w
x4≥300(1−w)
w∈{0,1}
These three constraints ensure that at least one of the corners 1 and 4 must be illuminated with at least 300 units of illumination.
xi≤150+150(1−zi)∀i∈{1,…,5}
∑i=15zi≥3
zi∈{0,1},∀i∈{1,…,5}
These three constraints ensure that at least three or more of the corners must be illuminated by 150 units of illumination or less. To see that, if zi=1, then the corresponding corner i will need to have less than 150 units of luminosity. However, if zi=0, then the corresponding constraint becomes xi≤300, which will be satisfied anyway since the maximum luminosity we can have at an intersection is 300.∑i=15zi≥3 ensures that at least three intersections will have this “less than 150 units of luminosity” requirement.
0.6x1−0.4x3≤0
This constraints is derived from the fractional constraint x1(x1+x3)≤0.4, where x1 is the luminosity at intersection 1 and x1+x3 is the luminosity of corridor B. We then multiply x1+x3 on both sides of the inequality (since we know that x1+x3 is strictly positive), we get this linear constraint.
The solution (x∗,y∗) can remain a unique optimal solution. This situation occurs, for example, if the change in the costs is very small.
The solution (x∗,y∗) remains optimal, but there are multiple optimal solutions. This situation can occur if the change in the costs is “just right.” For example, if the cost function changed to ‘‘z=2R+2G”, then the solutions (5, 3) and (2, 6) are both optimal, as are all of the solutions on the edge joining these two points.
A solution other than (x∗,y∗) is the unique optimal solution. This situation can happen if, for example, one cost coefficient changes a lot. If the objective were ‘‘z=.1R+2G”, the optimum solution would be (2, 6).
Shadow Price
The purpose of this week is how to get an additional information without re-solving the probrem.
For this problem, the problem of Max is equal to that of Max . Furthermore, the latter has the same solution as Max (The value of objective function would be different but the and are the same).
We have the sensitivity report for Max and know the range of the coefficient for not changing the solution (i.e. allowable increase/decrease of in the sensitivity report).
Changing Coefficients
The correct answer is 2. We are changing two RHS coefficients. By the 100% rule, we divide all allowable changes of RHS coefficients in the SR by 2. After dividing by 2, we see that the allowable increases of 2 for production capacity and 15 for warehouse capacity are allowed. The change in the optimal objective value is (2×11/14)+(15×1/35)=11/7+3/7=2.
Pricing Out
The correct answer is -1.0.
We change the capacity coefficient from 10 to 22. To determine the reduced cost, we can then subtract the product of the constraint coefficients and shadow prices from the cost coefficient, resulting in 6−(8×1114)−(22×135)=42070−44070−4470=−6470=−0.91
Computing Allowable Change
Reduced costs and pricing out
The reduced cost of a variable (say x 3 ) is the shadow price of its nonnegativity constraint, i.e., the constraint “x 3 ≥ 0.” The reduced cost of x 3 is the change in the optimal objective value if we change the constraint to “x 3 ≥ 1.”
Let z * denote the max objective value. Suppose we require x j ≥ p for some p > 0. Then the feasible region gets smaller. Let z’ be the max objective value for the modified problem. Then z’ ≤ z * , and thus c̄ j ≤ 0.
The of a “≥” for a maximization problem Let c̄ shadow j denote the reduced cost of x j for a maximization problem. problem is non-positive. • c̄ j is the shadow price of “x j ≥ 0.” The • shadow price of a “≤” for a maximization problem c̄ j ≤ 0. Can you see why? problem is non-negative.
Consider the glass problem, with the following adjustment. Suppose instead that the coefficient for production capacity for champagne glasses decreased from 8 to 7, and simulataneously the coefficient for storage increased from 10 to p.
For what values of p is it worth producing champagne glasses?
The correct answer is:
‘‘p≤17.5.” If we price out champagne glasses, the reduced cost is 6−7×(11/14)−p×1/35=.5−p/35. This value is non-negative whenever p≤17.5.
It should increase by 4857.14. To determine the allowable increases when two cost coefficients change, one needs to divide the allowable increases by 2 (using the 100% rule). The number of cameras and memory sticks produced does not change because we remain within the (modified) allowable increase/decrease region suggested by the sensitivity report.
Reducing the number of Test Device 3 hours by 50 could affect total revenue, but we do not have enough information to compute the magnitude of the change. The allowable decrease is is 2342.86, or 39 hours, which the suggested 50 hour reduction exceeds.
We remain within the allowable decrease region for cameras, and reduce the profit by the product of the unit decrease and number of units. The new optimal profit is 125×171.4285714+135×800, which is approximately 129428.57.
For a single unit, we have 92−12×20=−148. One should also subtract the coefficient for circuit boards in other constraints times the shadow prices. However, the shadow prices for Test Device 2 capacity and Test Device 3 capacity are both 0. And the shadow price on the upper bound for circuit boards is also 0.
Using the special case of the 100% rule given in 15.053x, we need to divide the allowable increases and decreases by 2. The revised allowable increase for device 1 availability is 1640. The revised allowable decrease for circuit board demand is 350. Thus, the combined change in RHS is within the revised limits. The change in objective follows is 1000× [shadow price for device 1] −200× [shadow price for circuit board demand]. This is equal to 1000×20=20000.
The extreme points are (0,1),(1,0),(0,2),(2,0),(4/3,4/3) and the optimum value of −4 is achieved at (0,1). Tracing out the simplex algorithm depends on where you start. If you happen to start from the extreme point (2,0), the simplex algorithm will either trace (1,0),(0,1) or (4/3,4/3),(0,1) in order.
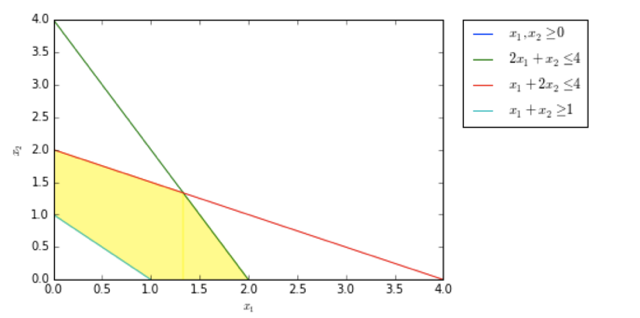
Suppose that the objective function is changed to z=−x1+cx2. Graphically determine the values of c for which the solution found in part (a) remains optimal
The correct answer is:
−1≤c≤0
For −1≤c≤0, the extreme point (0, 1) is optimal. For c=0 the optimum extreme points are (0,1) and (0,2). For c>0, (0,1) is not optimal anymore. Similarly, for c=−1, (0,1) and (1,0) are both optimal. For c<−1, (0,1) isn’t optimal anymore.
#######
Excerpted from: Dimitris Bertsimas and John N. Tsitsiklis, Introduction to Linear Optimization, Athena Scientific, 1997, Exercise 5.8. We thank the authors for permitting us to use this problem.